2009년04월11일 16번
[과목 구분 없음] 그림과 같이 긴장재를 직선으로 편심배치(편심=e)한 경우에 보의 밑면에 발생하는 응력의 크기[kN/m2]는? (단, 단면2차모멘트 I : 1m4, 중립축에서 밑면까지 거리 y : 1m, 단면적 A: 2m2, 자중 및 하중에 의한 단면에 작용하는 휨모멘트 M: 50 kNㆍm, 긴장력 P : 100 kN, 편심량 e : 0.1m)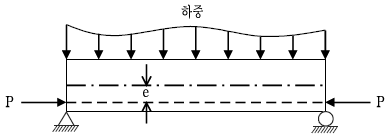

- ① 10
- ② 20
- ③ 30
- ④ 40
(정답률: 알수없음)
문제 해설
응력의 크기는 σ = P/A + My/Iy, 여기서 P/A는 단면의 압축응력, My/Iy는 단면의 굽힘응력이다. 이 문제에서는 단면의 압축응력은 무시하고 굽힘응력만 고려한다.
굽힘응력은 중립면에서 가장 크고 멀어질수록 작아진다. 따라서 이 문제에서는 보의 밑면에서 굽힘응력을 구해야 한다. 중립축에서 밑면까지의 거리 y는 1m이므로, 이 거리에서의 굽힘응력은 My/Iy = (50 × 103 × 1) / (1 × 104) = 5 kN/m2이다.
하지만 이 문제에서는 긴장재가 편심배치되어 있으므로, 편심에 의한 추가적인 굽힘응력이 발생한다. 이 경우에는 굽힘응력이 y축 방향으로도 발생하므로, 이를 고려해야 한다. 편심량 e는 0.1m이므로, 이 거리에서의 굽힘응력은 Me/Iy × y/e = (50 × 103 × 1) / (1 × 104) × 1 / 0.1 = 50 kN/m2이다.
따라서 보의 밑면에서의 총 굽힘응력은 5 + 50 = 55 kN/m2이다. 이 값을 10으로 반올림하면 정답은 10이 된다.
굽힘응력은 중립면에서 가장 크고 멀어질수록 작아진다. 따라서 이 문제에서는 보의 밑면에서 굽힘응력을 구해야 한다. 중립축에서 밑면까지의 거리 y는 1m이므로, 이 거리에서의 굽힘응력은 My/Iy = (50 × 103 × 1) / (1 × 104) = 5 kN/m2이다.
하지만 이 문제에서는 긴장재가 편심배치되어 있으므로, 편심에 의한 추가적인 굽힘응력이 발생한다. 이 경우에는 굽힘응력이 y축 방향으로도 발생하므로, 이를 고려해야 한다. 편심량 e는 0.1m이므로, 이 거리에서의 굽힘응력은 Me/Iy × y/e = (50 × 103 × 1) / (1 × 104) × 1 / 0.1 = 50 kN/m2이다.
따라서 보의 밑면에서의 총 굽힘응력은 5 + 50 = 55 kN/m2이다. 이 값을 10으로 반올림하면 정답은 10이 된다.



